Date de publication : 30/01/2010.
Par
Pierre Lecomte (articles mathématiques)
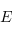de dimension finie sur un corps 
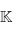et muni d'une
forme bilinéaire non dégénérée 
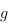. Si la caractéristique de 
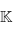est différente de deux,
alors les images des endomorphismes antisymétriques de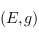 
sont de dimension paire.
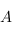est antisymétrique si la forme bilinéaire 
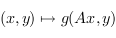est antisymétrique.
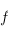la forme bilinéaire antisymétrique 
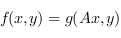. Le rang de 
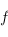est égal
au rang de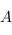 
. De plus, il est bien connu et facile de montrer par récurrence qu'il existe une base dans laquelle la matrice
de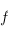 
est diagonale par blocs, chaque bloc étant nul ou bien égal à
.
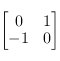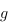. Soient 
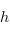et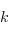 
les applications de 
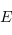dans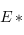 
définies par 
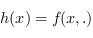et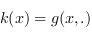 
.
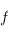est égal à celui de 
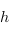. Or, 
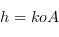et
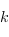est un isomorphisme, donc le rang de 
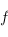est égal à celui de 
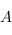. Maintenant, on oublie
complètement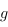 
et on doit montrer que le rang 
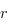de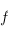 
est pair.
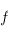est égal au rang de la matrice 
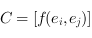pour toute base 
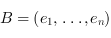de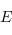 
(en effet, 
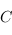est la matrice de 
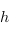dans les bases 
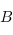et
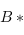, où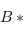 
désigne la base duale de 
).
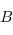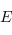par un supplémentaire du noyau 
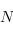de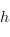 
, on peut supposer que
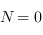, donc 
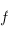est non dégénérée, ce qui entraîne que 
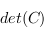est non nul. Or,
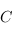est antisymétrique donc 
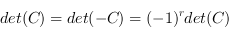, ce qui montre que 
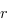est pair.
Copyright © 2010 Pierre Lecomte. Aucune reproduction, même partielle, ne peut être faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc. sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts. Droits de diffusion permanents accordés à Developpez LLC.
